MWD: Theories¶
MWD Discretization¶
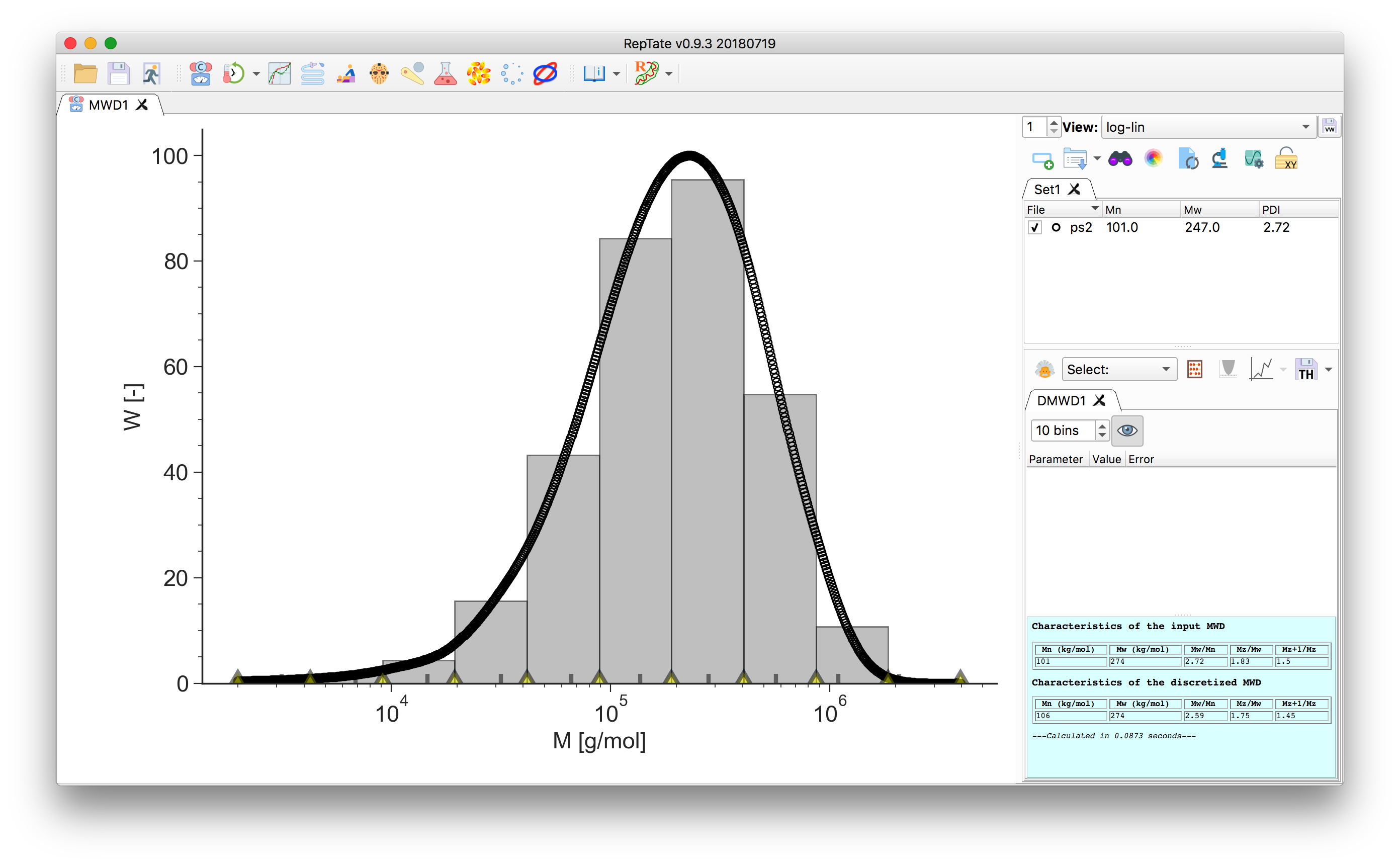
The area, \(\phi_i\), of each grey bin corresponds to the area under the data curve delimited by the bin edges. The height, \(h_i\), of the bin is the area divided by the bin width (on a \(\log_{10}\) scale).
You can change the number of bins and move the bin edges by dragging the yellow markers.
In the bottom of the plot, the grey tick marks indicate the bin molecular weight taken as the weight-average molecular mass value across the bin width
\[M_{w,i} = \frac{\sum w_j M_j}{\sum w_j}.\]
To save the discretized molecular weight, click the
 button.
button.The output file contains a header with the moments \(M_n\), \(M_w\) and the PDI, and two columns. The first column is the molecular weight \(M_{w,i}\) as indicated by the grey tick marks, the second column is \(\phi_i\), the value of the area of the covered by the bin.
The sum of the areas should equal 1:
\[\sum \phi_i = 1.\]
Log-Normal distribution¶
Summary¶
Log-Normal distribution: the logarithm of the molecular weight is normally distributed
- Function
- \[W(M) = W_0 \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left[ - \frac{\left(\ln{M}-(\ln{M_0} + \sigma^2)\right)^2}{2\sigma^2} \right]\]
- Parameters
logW0\(\equiv\log_{10}(W_0)\): Normalization constant.logM0\(\equiv\log_{10}(M_0)\)sigma\(\equiv\sigma\)
Generalized Exponential Function¶
Summary¶
Generalized Exponential Function (GEX) for experimental molecular weight distributions.
- Function
- \[W(M) = W_0 \frac{b}{M_0 \Gamma\left(\frac{a+1}{b}\right)} \left(\frac{M}{M_0}\right)^{a} \exp\left[ -\left(\frac{M}{M_0}\right)^b \right]\]
- Parameters
logW0\(\equiv\log_{10}(W_0)\): Normalization constant.logM0\(\equiv\log_{10}(M_0)\): Proportional to \(M_n\) and \(M_w\).a: Parameter related to polydispersity and skewnessb: Parameter related to polydispersity and skewness