LVE: General Description¶
Purpose¶
Application to Analyze Linear Viscoelastic Data
Data Files¶
The first line of the file should contain the sample parameters separated by semi-colons (
;). It may contain any number of parameters which will be read and saved as file-parameter in RepTate.Then the data columns should appear, separated by spaces or tabs.
.tts extension¶
Text files with .tts extension should be organised as follows:
.ttsfiles should contain at least the parameter values for the:sample molar mass
Mw,temperature
T.
3 columns separated by spaces or tabs containing respectively:
frequency, \(\omega\),
elastic modulus, \(G'\),
loss modulus \(G''\).
Other columns will be ignored. A correct .tts file looks like:
T=-35;CTg=14.65;dx12=0;isof=true;Mw=13.5;chem=PI;PDI=1.04;
1.90165521264016E+0000 7.38023647054321E+0001 1.35152457625702E+0004 -2.99910000000000E+0001
3.01392554124040E+0000 1.99063258930248E+0002 2.14834778959042E+0004 -2.99900000000000E+0001
4.51700049635957E+0000 3.72861375546198E+0002 3.17756716623334E+0004 -3.99960000000000E+0001
... ... ... ...
Views¶
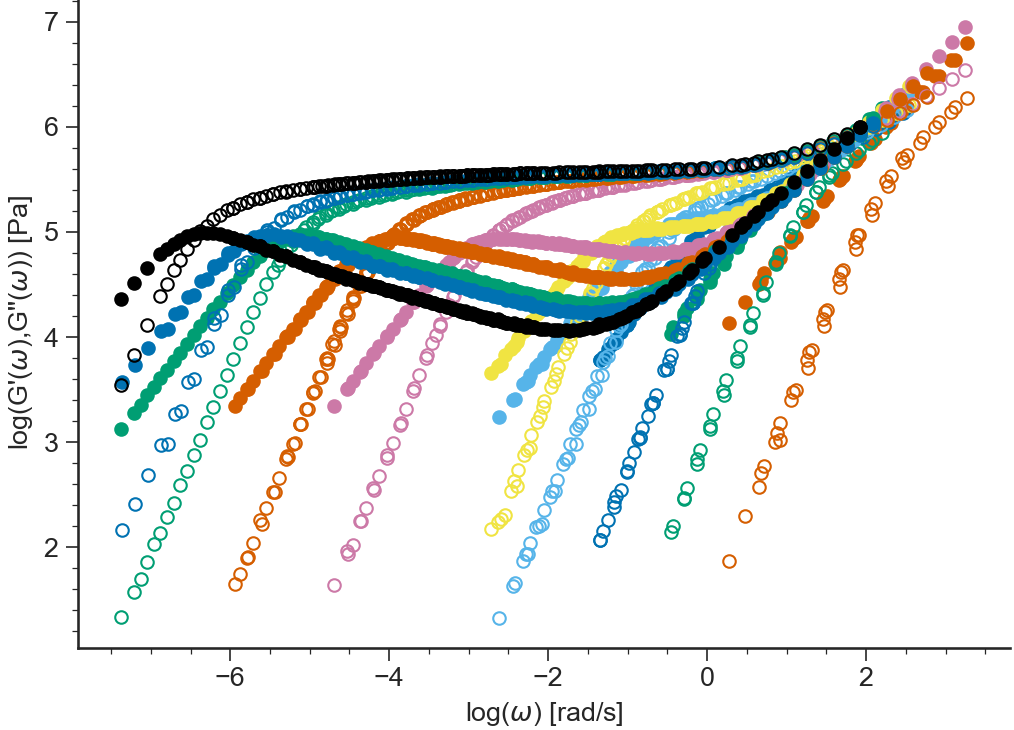
log(G’,G”(w))¶
- ApplicationLVE.viewLogG1G2()[source]¶
Logarithm of the storage modulus \(\log(G'(\omega))\) and loss modulus \(\log(G''(\omega))\) vs \(\log(\omega)\)
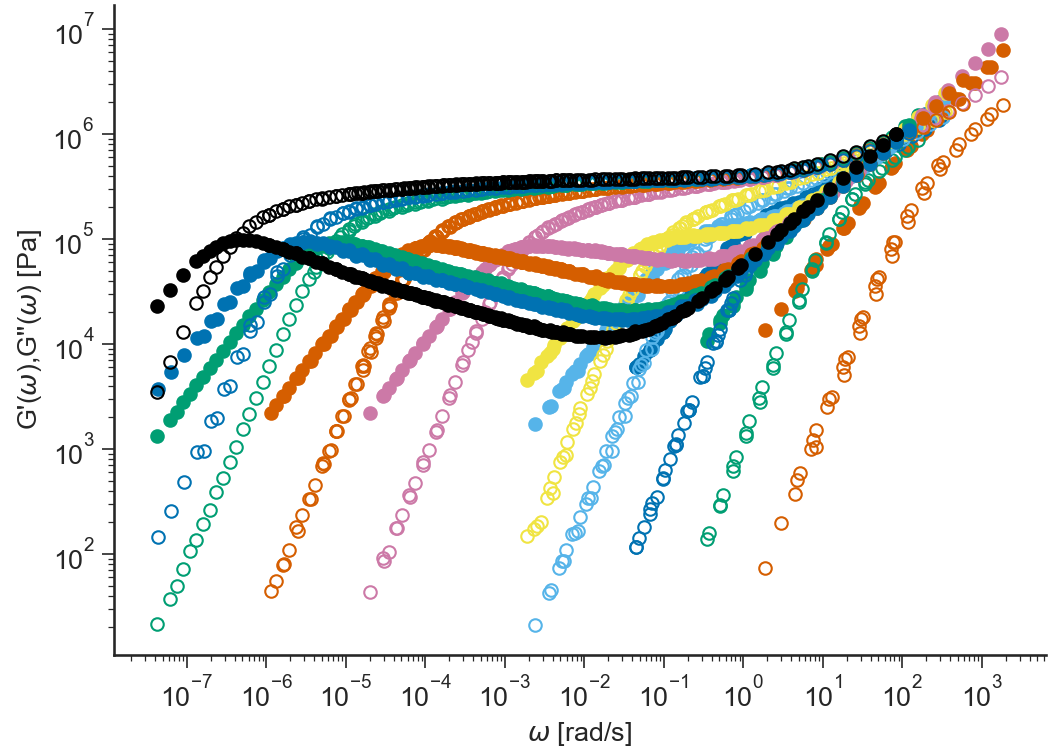
G’,G”(w)¶
- ApplicationLVE.viewG1G2()[source]¶
Storage modulus \(G'(\omega)\) and loss modulus \(G''(\omega)\) (in logarithmic scale) vs \(\omega\) (in logarithmic scale)
etastar¶
- ApplicationLVE.viewEtaStar()[source]¶
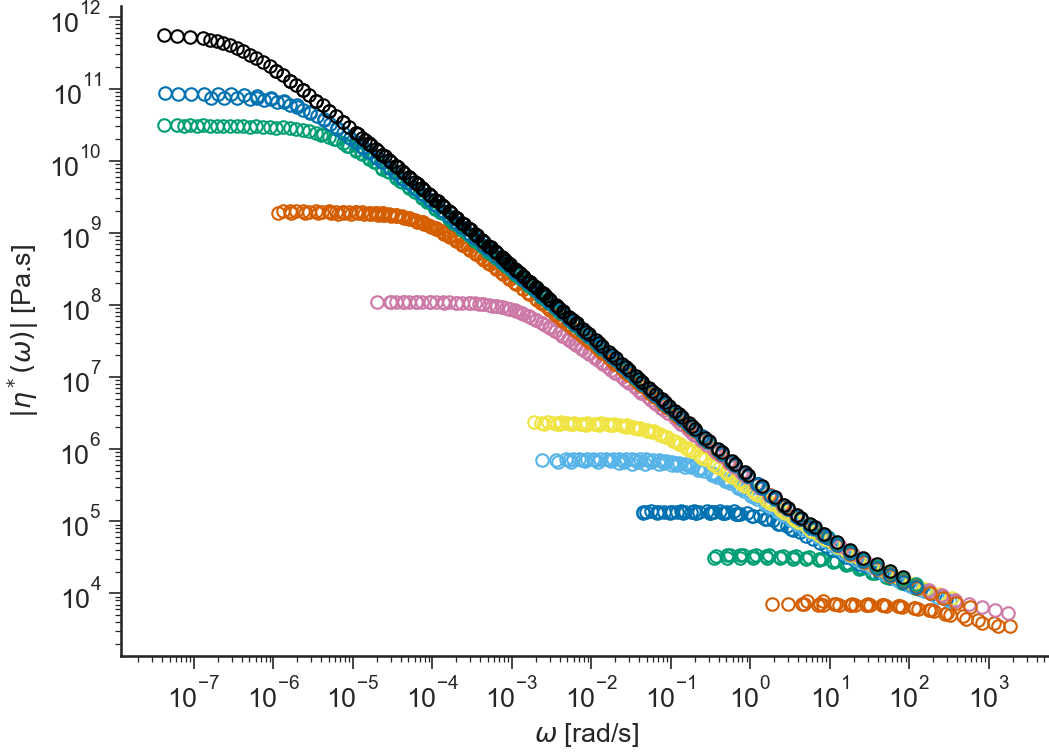
Complex viscosity \(\eta^*(\omega) = \sqrt{G'^2 + G''^2}/\omega\) (in logarithmic scale) vs \(\omega\) (in logarithmic scale)
logetastar¶
- ApplicationLVE.viewLogEtaStar()[source]¶
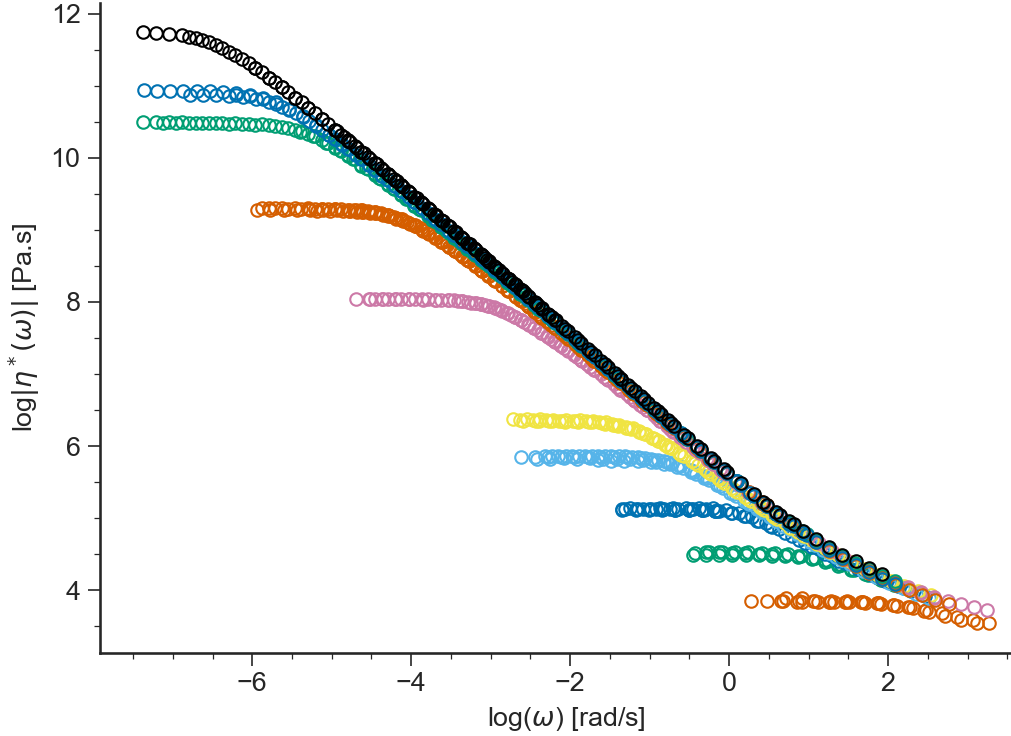
Logarithm of the complex viscosity \(\eta^*(\omega) = \sqrt{G'^2 + G''^2}/\omega\) vs \(\log(\omega)\)
delta¶
- ApplicationLVE.viewDelta()[source]¶
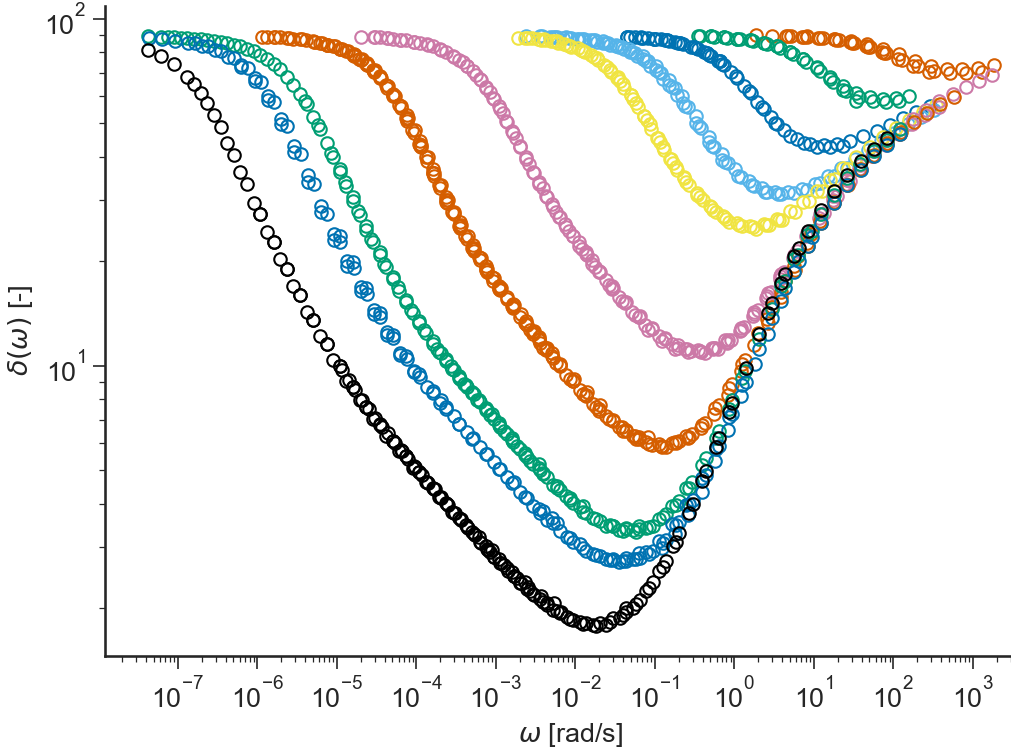
Loss or phase angle \(\delta(\omega)=\arctan(G''/G')\cdot 180/\pi\) (in degrees, in logarithmic scale) vs \(\omega\) (in logarithmic scale)
tan(delta)¶
- ApplicationLVE.viewTanDelta()[source]¶
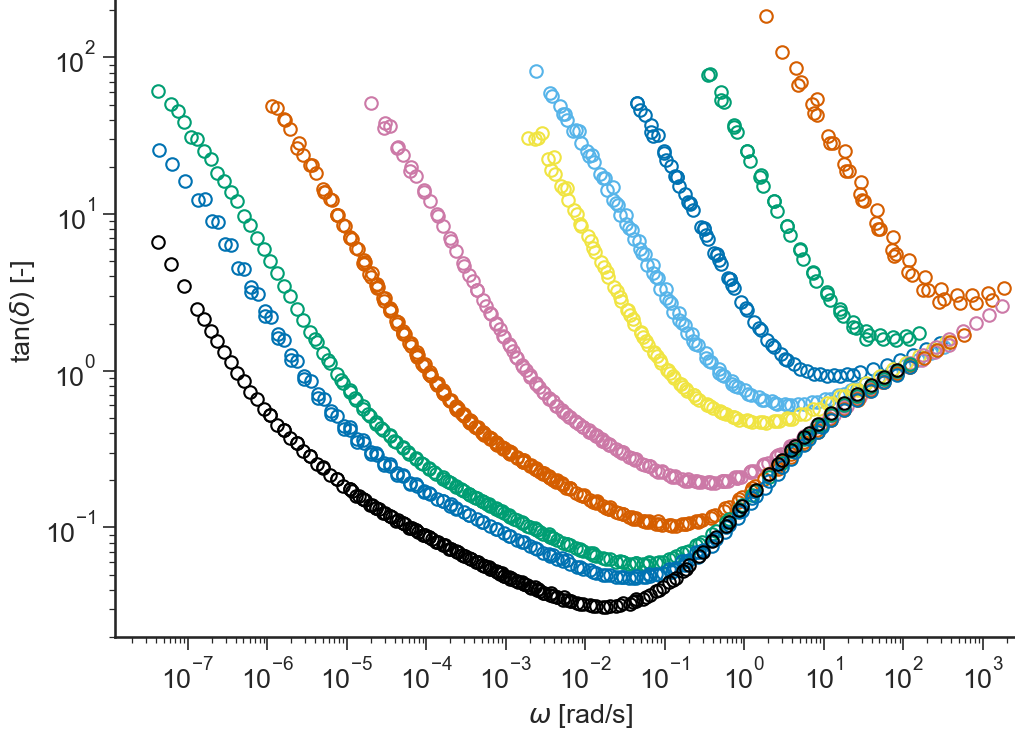
Tangent of the phase angle \(\tan(\delta(\omega))=G''/G'\) (in logarithmic scale) vs \(\omega\) (in logarithmic scale)
log(tan(delta))¶
- ApplicationLVE.viewLogTanDelta()[source]¶
\(\log(\tan(\delta(\omega)))=\log(G''/G')\) vs \(\log(\omega)\)
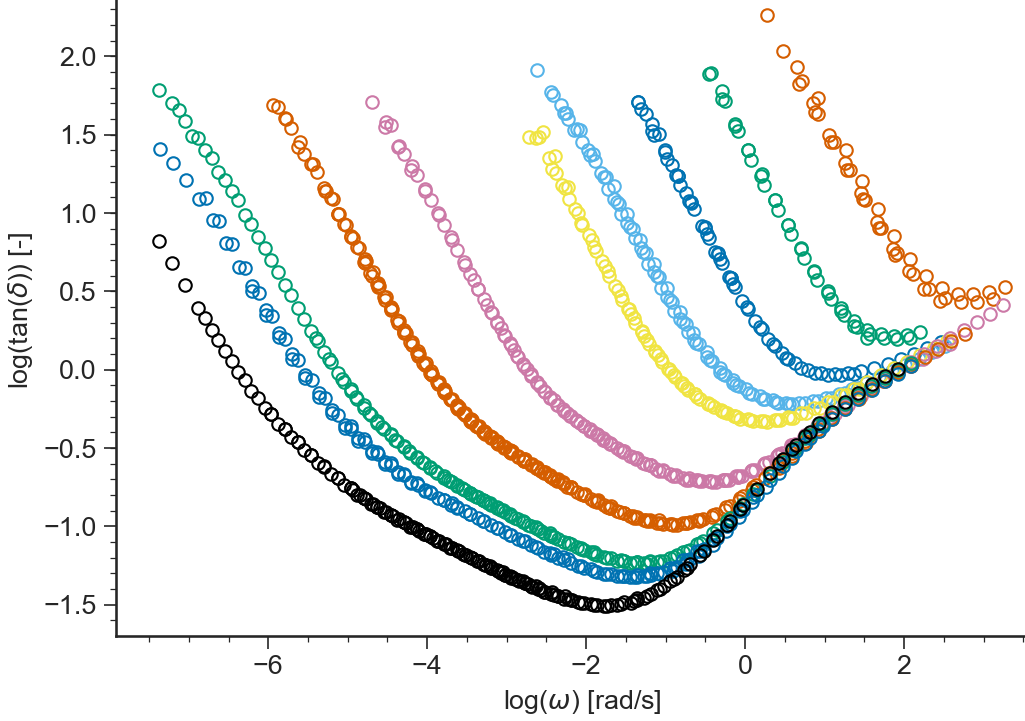
log(G*)¶
- ApplicationLVE.viewLogGstar()[source]¶
Logarithm of the modulus of the complex viscosity \(|G^*(\omega)|=\sqrt{G'^2+G''^2}\) vs \(\log(\omega)\)
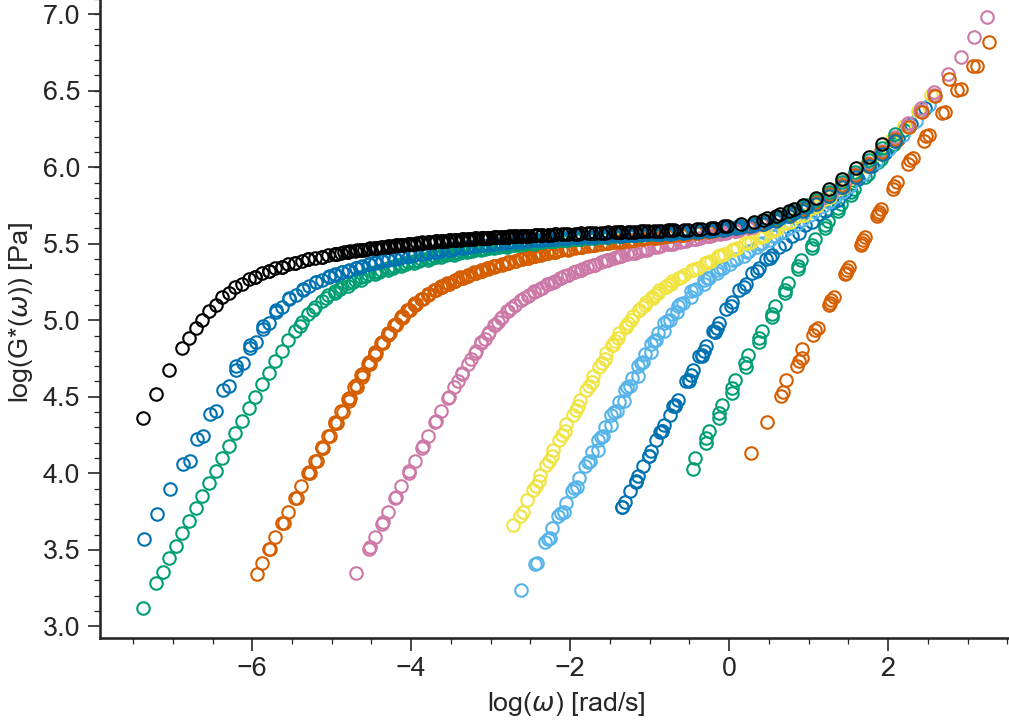
log(tan(delta),G*)¶
- ApplicationLVE.viewLogtandeltaGstar()[source]¶
Logarithm of the tangent of the loss angle \(\tan(\delta(\omega))=G''/G'\) vs logarithm of the modulus of the complex viscosity \(|G^*(\omega)|=\sqrt{G'^2+G''^2}\)
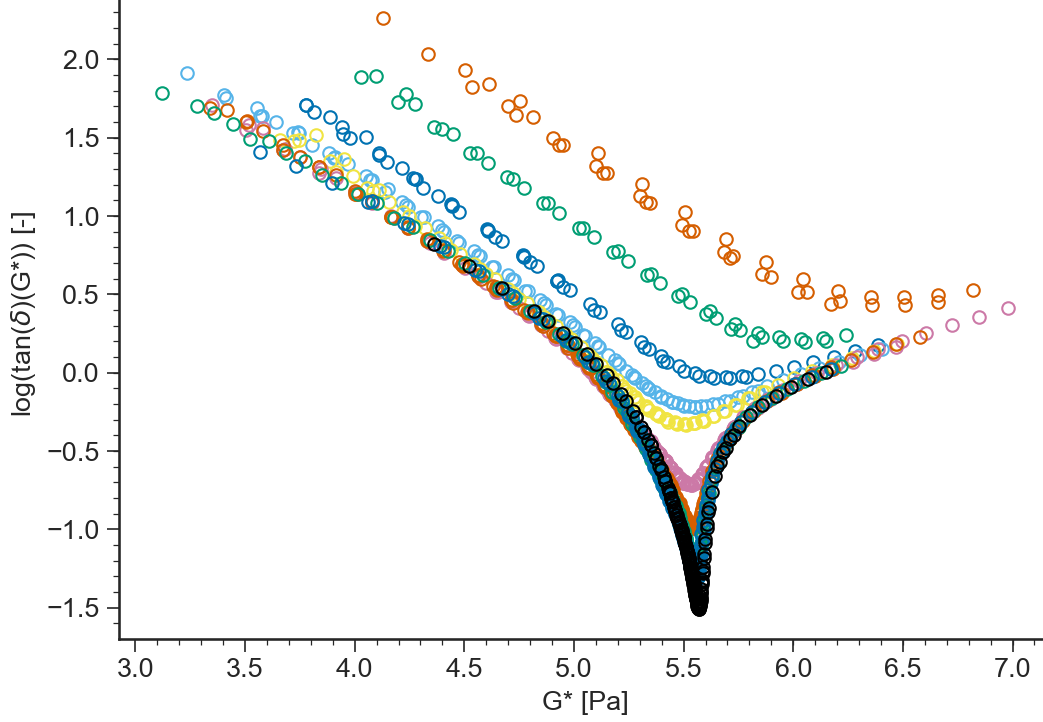
delta(G*)¶
- ApplicationLVE.viewdeltatanGstar()[source]¶
Loss angle \(\delta(\omega)=\arctan(G''/G')\) vs logarithm of the modulus of the complex viscosity \(|G^*(\omega)|=\sqrt{G'^2+G''^2}\)
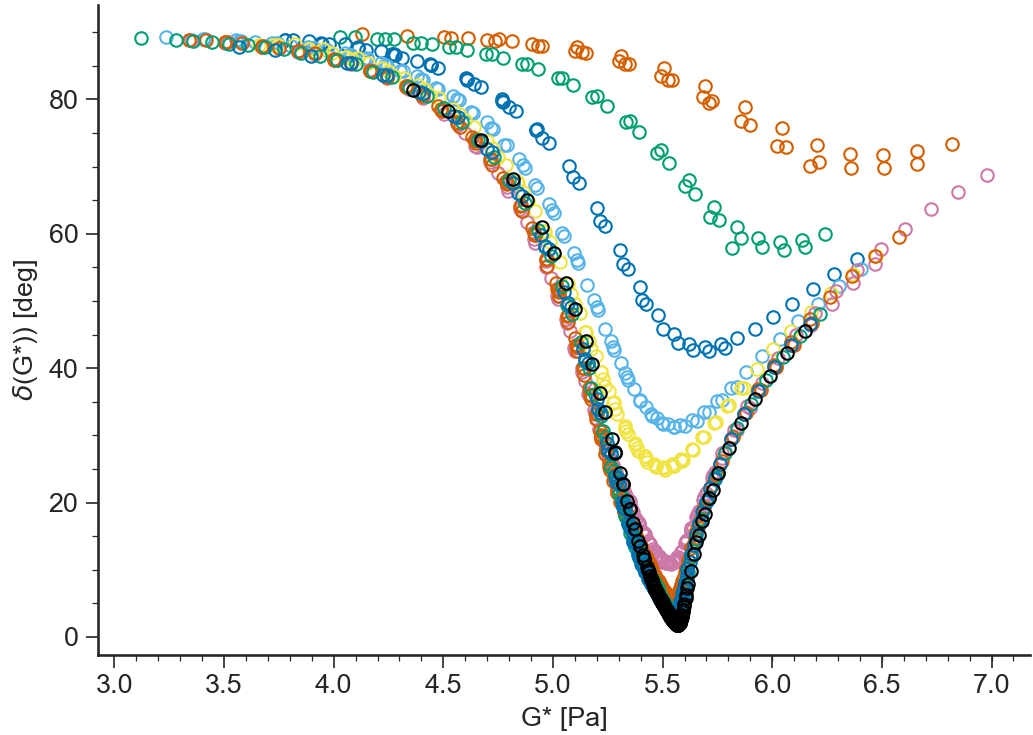
J’,J”(w)¶
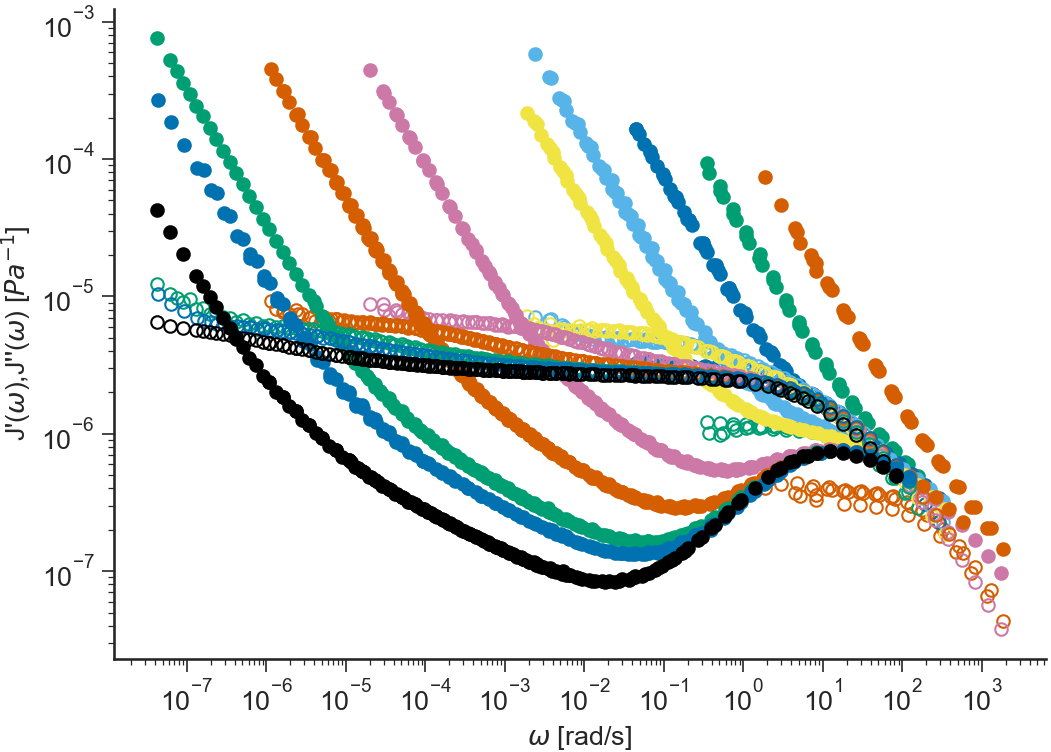
- ApplicationLVE.viewJ1J2()[source]¶
Storage compliance \(J'(\omega)=G'/(G'^2+G''^2)\) and loss compliance \(J''(\omega)=G''/(G'^2+G''^2)\) (in logarithmic scale) vs \(\omega\) (in logarithmic scale)
Cole-Cole¶
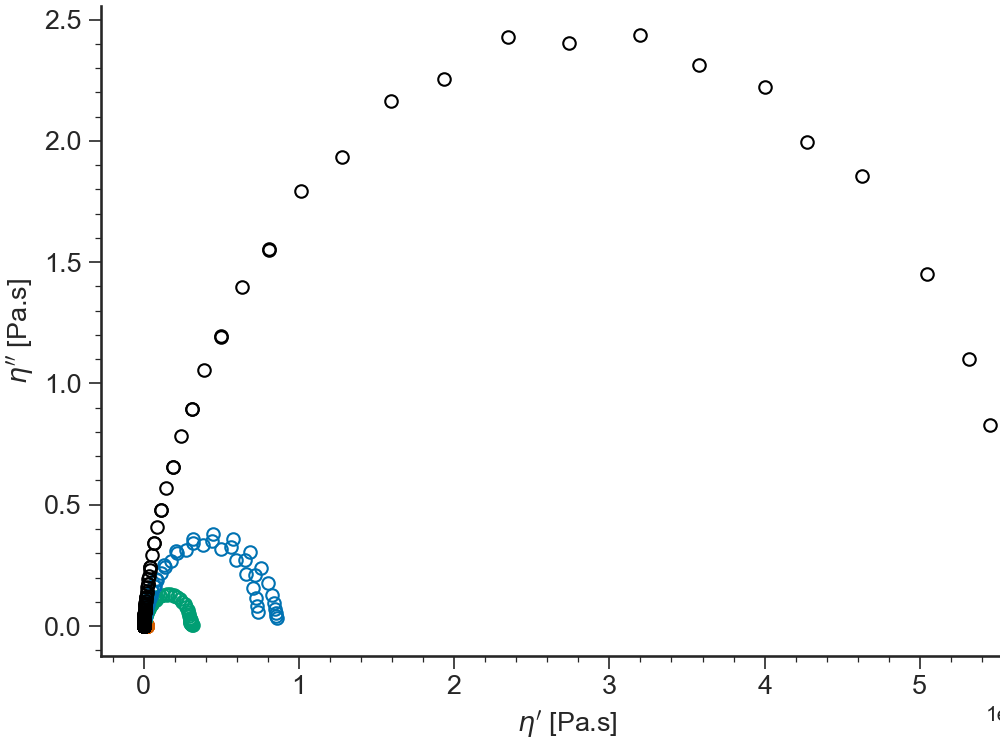
- ApplicationLVE.viewColeCole()[source]¶
Cole-Cole plot: out of phase viscosity \(\eta''(\omega)=G'(\omega)/\omega\) vs dynamic viscosity \(\eta'(\omega)=G''(\omega)/\omega\)
log(G’)¶
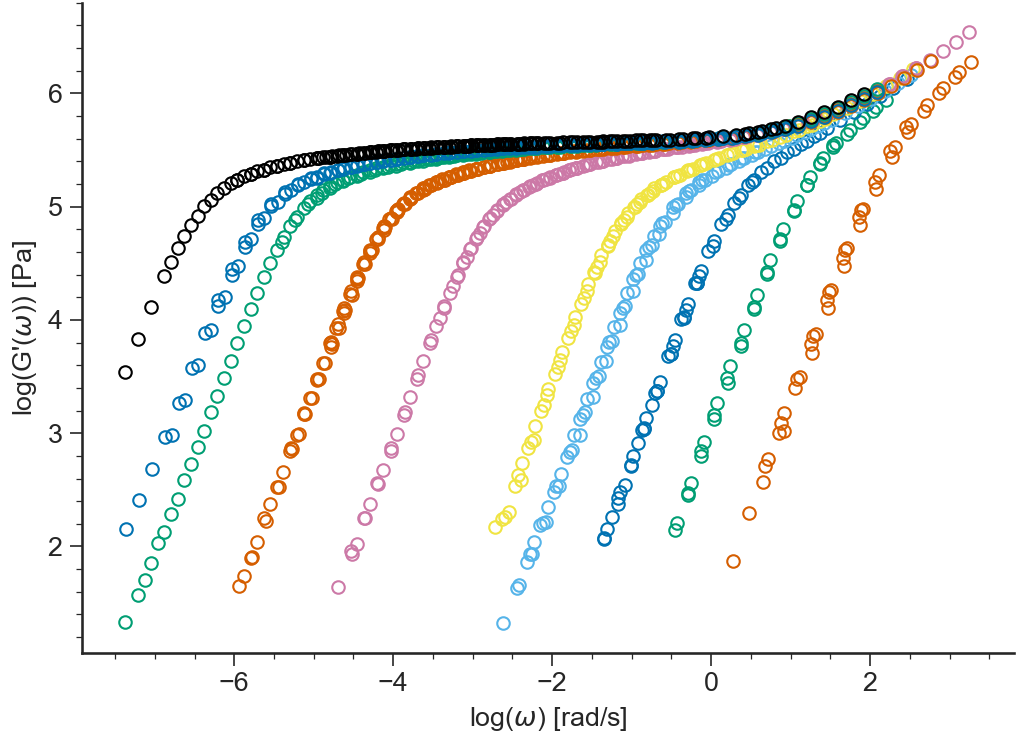
- ApplicationLVE.viewLogG1()[source]¶
Logarithm of the storage modulus \(\log(G'(\omega))\) vs \(\log(\omega)\)
G’¶
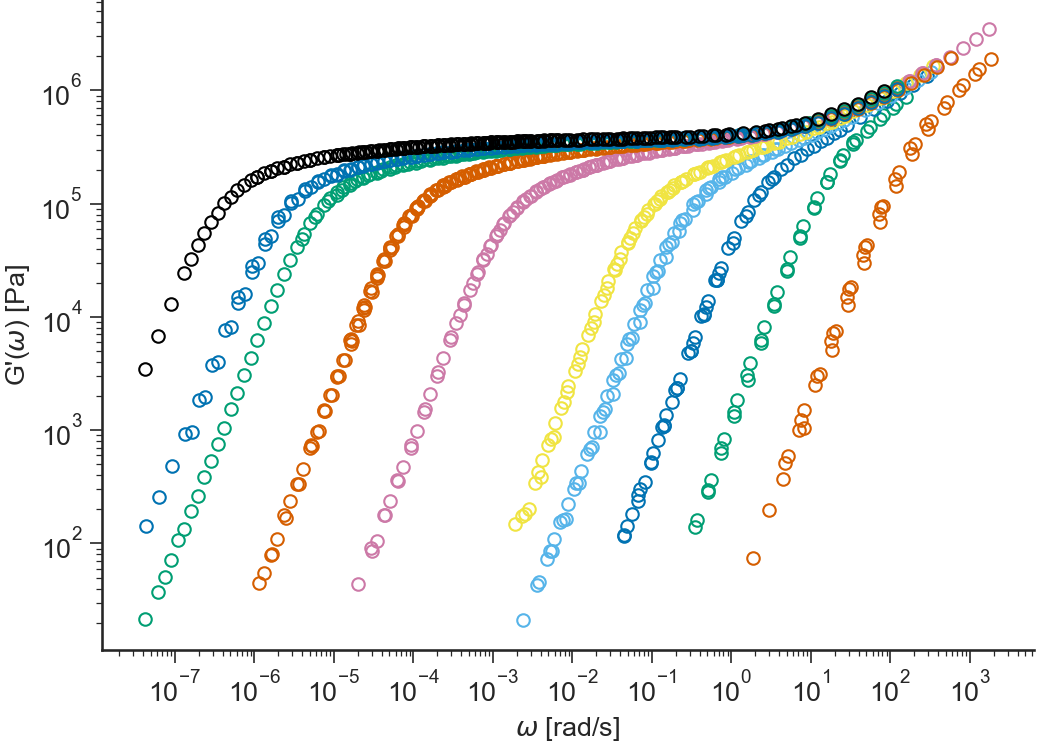
- ApplicationLVE.viewG1()[source]¶
Storage modulus \(G'(\omega)\) (in logarithmic scale) vs \(\omega\) (in logarithmic scale)
log(G”)¶
- ApplicationLVE.viewLogG2()[source]¶
Logarithm of the loss modulus \(\log(G''(\omega))\) vs \(\log(\omega)\)
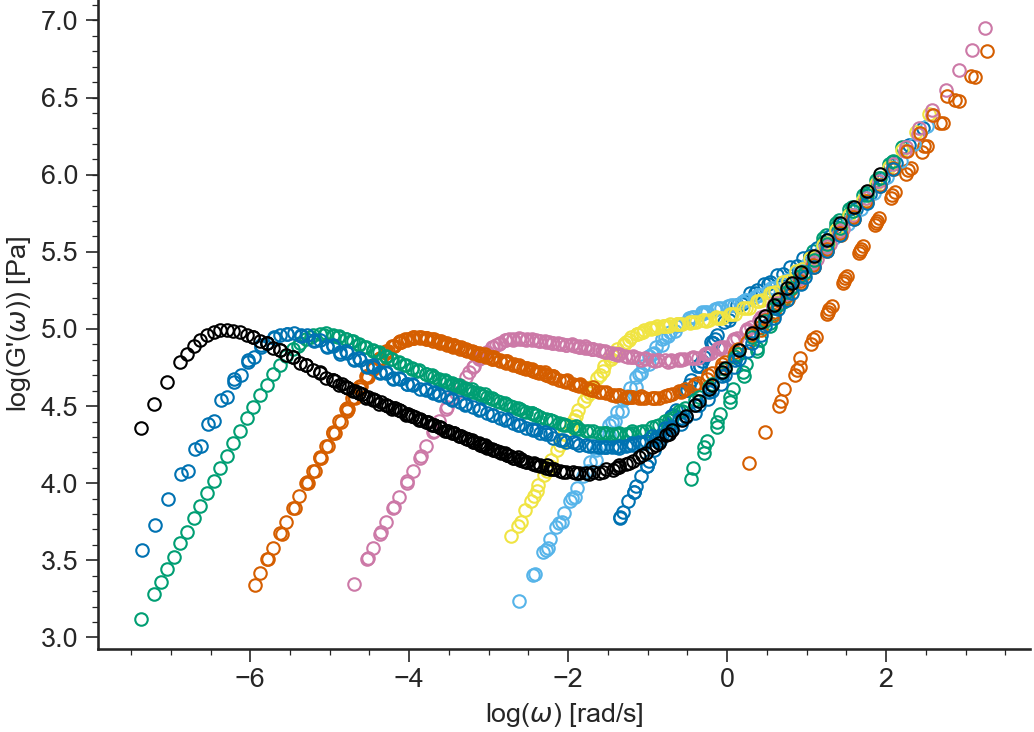
GӦ
- ApplicationLVE.viewG2()[source]¶
Loss modulus \(G''(\omega)\) (in logarithmic scale) vs \(\omega\) (in logarithmic scale)
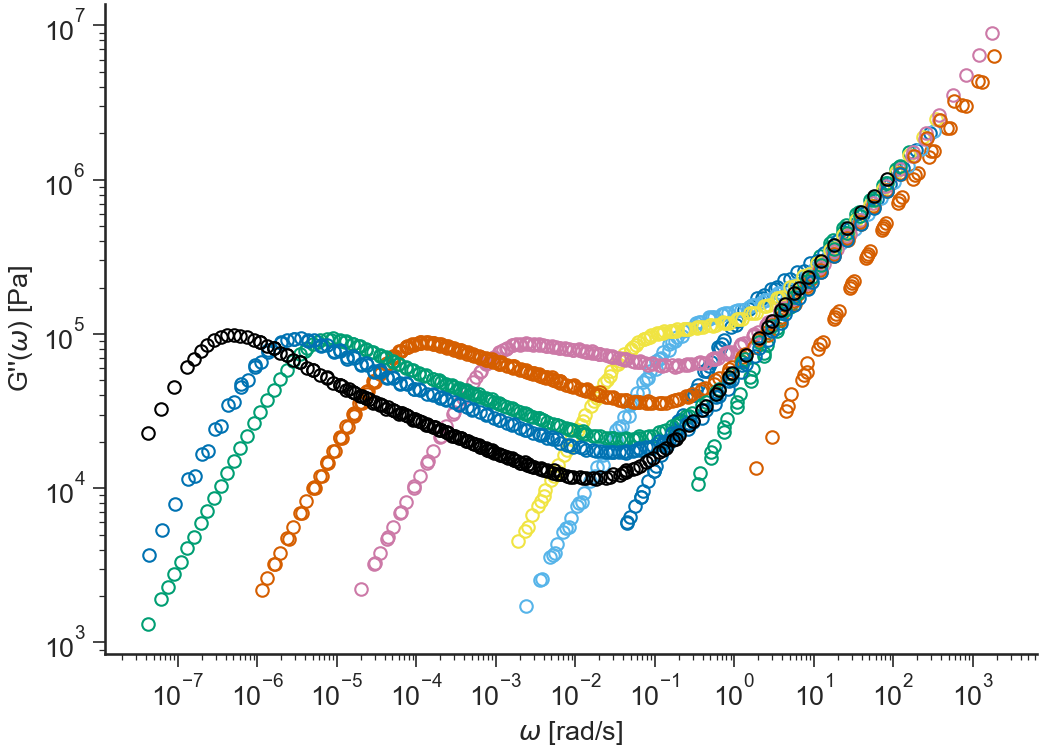
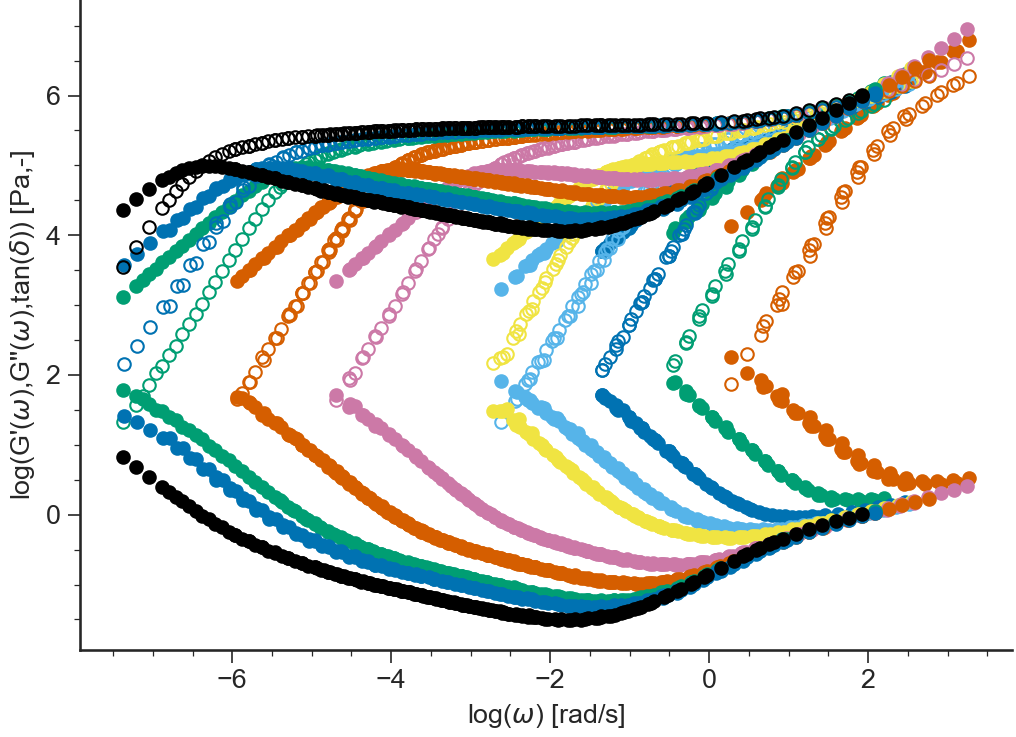
log(G’,G”(w),tan(delta))¶
- ApplicationLVE.viewLogG1G2tandelta()[source]¶
Logarithm of the storage modulus \(\log(G'(\omega))\), loss modulus \(\log(G''(\omega))\) and tangent of the loss angle \(\log(\tan(\delta(\omega)))=\log(G''/G')\) vs \(\log(\omega)\)